GPU 에 의해서 Rendering 이 어떻게 수행되는지 자세하게 Detail 들을 배워나갈 것이다.

주전가와 같은 polygon mesh 가 drawcall 에 의해서
GPU 내부로 들어간다.
Polygon Mesh 의 정점들은 vertex array 에 저장이 되어있을 것이다.
[ Vertex shader ] Shader라는 프로그램을 짜줘야지만 GPU 에서 실행된다.
Vertex array 에 저장된 정점들을 한번에 하나씩 불러들이면서 여러가지 연산을 수행한다.
[ Resterizer ] 하드웨어에 셋팅된 정해진 기능만 수행한다.
Index array 의 정보들을 이용해서 삼각형들을 다시 일단 조립을 한다.
이 삼각형은 픽셀들의 조합으로 되어있을텐데,
이 픽셀들의 정보를 ( 색상 ) Resterizer 가 모아서 각 픽셀 위치마다 저장을 해놓는다.
그 저장해 놓은것을 Fragment 라고 한다. ( 예비 픽셀, 후보픽셀 정도라고 이해해라.)
(래스터화된 이미지는 컴퓨터 디스플레이, 비디오 디스플레이 또는 프린터에 표시되거나 비트맵 파일 형식으로 저장될 수 있다.)
[ Fragmenet shader ] Shader라는 프로그램을 짜줘야지만 GPU 에서 실행된다.
Fragment 의 실제 컬러를 결정을 한다.
[ Output merger ] 하드웨어에 셋팅된 정해진 기능만 수행한다.
최종적으로 최종으로 결정된 색상을 보여줄지 말지 결정한다. 보여줘도 어떻게 보여줄지 결정을 한다.
[Shader]
쉐이더는 말그대로 프로그램이다. Vertex 에 적용해야 하는 연산을 우리가 원하는대로 작성할 수있다.
Object space에서 정의된 정점을 최종적으로 Clip space로 옮겨주는 것은 반드시 해야한다.
아래의 그림은 그 과정이다.

(tip) 4장에서 Vector 를 World Transform ( Vector들을 Object space -> World space로 옮기는 과정 )하는 방법을 배웠음.
이제 Vector normals를 World transform 하는 것을 배워야한다.
[ Vector normals World Trasform - 법선벡터의 월드 변환 ]
4장에서 Vertex의 position의 World Transform 은 Affine Transform(S,R,T) 을 통해 만들어 냈었다.
Vertex의 position 의 World Transform 은 즉, [L|T]로 표현할 수 있다.
★그렇다면 Vertex 의 normals(법선벡터)의 World Transform 은 ?
결과적으로, L의 inverse, transpose ( 역행렬의 전치행렬) 에 n(법선벡터) 곱해주면 된다. 그리고 normalized 해주면 끝.
☆ 아래는 그것을 증명해 보이도록 할것이다.
Vertex Normals 에 월드변환을 적용해보자.
ㄴ vn = [L|T]n 이렇게 된다.
[L|T]n = Ln + T ( ∵ 벡터는 움직여봐야 동일하다. 그래서 T는 생각하지 않아도 된다. )
∴ Ln을 통해 법선벡터의 world Transform 을 만들어 낼 수 있다.
[ Non uniform 한 scaling 의 경우]
ex_1 ) 여기서 Linear tranform 이 non uniform 한 scaling 이라면 ???? ( non uniform scaling 예시 (1/2, 1/2, 2) )
qna) non uniform 한 scaling그대로 Ln에 적용하면 되는가?
ans) 안된다. non uniform 한 scaling 이라면 , 법선벡터가 이상해진다.
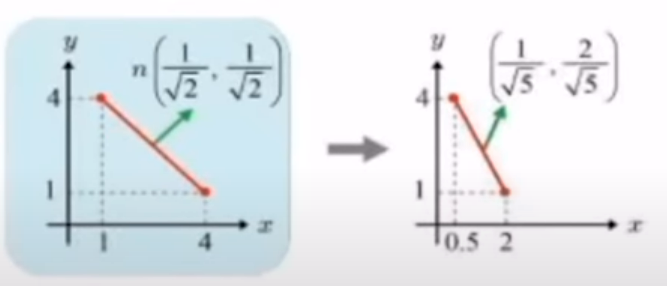
ex_2) non uniform 한 sacling 일때 올바른 Ln 구하는 방법
L 의 Inverse(역행렬)에 Transpose( 전치행렬)를 해주어야 한다.
그리고 나서 Ln 에 적용해서 world transform 된 법선벡터를 구해야한다.

ex_3 ) uniform scaling 한 법선벡터의 worldtransform 도 ex_2처럼 하면 안되나?
된다. 그러니까 그냥 L^(-1T) 로 통일하자.
[Shader]
쉐이더는 말그대로 프로그램이다. vertex 에 적용해야 하는 연산을 우리가 원하는대로 작성할 수있다.
object space에서 정의된 정점을 최종적으로 clip space로 옮겨주는 것은 반드시 해야한다.

우리는 World transform 까지 할 줄 알게 되었다. 이제, View transform 을 배우러 가보자.
tip ) 모든 vertex 는 World space 의 좌표를 가진다. 하지만, 이를 렌더링(그리는데) 사용하려면 어렵다. Camera Space 는 비교적 랜더링 알고리즘을 개발하는데 쉽다. 그래서 Camera Space 로 옮겨서 Camera Space 의 좌효표를 얻는 view transform 이 필요하다.
[View Transform]
World space가 있을때, 그 월드공간을 어디서 어떻게 볼것인지 결정한 Camera Space 에서 바라보도록 하는 Transform ( 변환 ) 이다.
[ EYE ]
Camera 가 어디서 볼것인가
[Look AT]
내가 기준으로 삼는 점의 3차원 좌표가 필요하다.
[UP]
카메라가 얼마나 기울어지는지 체크하기 위한 up 벡터가 제공된다.
[Camera Space]
( u, v, n )은 orthonormal 한 축이고, Eye라는 원점까지 있다면 ,그야말로 space의 필요충분조건을 다갖추지 않았는가! 그것을 camera space라고 한다.

[Camera Space의 (u,n,v) 구하기]
카메라 스페이스를 다음과 같이 표현했을때 ( u, n, v , Eye(origin) )
우리는 Camera Space 의 u,n,v 벡터를 주어진 Eye, At, Up 세개의 벡터로 구해낼 수 있다.
Cross product를 이용해서 구하는 것이다. (오른손의 법칙)

[ At 을 Camera Space 로 표현해보자]
EYE를 기준으로 At의 벡터 방향은 ( 0, 0 , -n ) 이 된다.
EYE를 기준으로 At까지의 길이가 10이라고 하면
AT 은 ( 0, 0 , -10 ) 이 될것이다.
이것을 world space 에 있는 At vertex 를 camera space 좌표계로 표현한 방법이다.
[View Transform (Camera Space 좌표를 얻는) 과정]
1. Camera Space을 World space에 포개지도록 한다.
- 원점이 다르므로 translation 을 한다. ( EYE 좌표를 원점좌표로 이동 )
- EYE좌표가 옮겨감 = Camera Space가 옮겨감 & 물체 또한 옮겨간다.

2 . (u, v, n) 을 (e1, e2, e3) 와 겹쳐지게 만든다.
- 이것은 Rotation 으로 하는것 ( 빨간색 박스는 , 밑밑 사진의 (b) 를 통해 이해하면 된다. )

- Rotation 은 어떻게 해야하는데?
이것은 4장 맨마지막에서 배웠었다. ( 아래 참고사진에서 (b) 과정 )
u,v,n 과 다른 방향을 가지는 축을 u,v,n 과 동일하게 맞추려면 전치행렬을 곱해주면 되었다.

[ View Transform 을 4x4 행렬 곱으로 나타내면? ]
world space 의 좌표에 아래의 것을 곱하면
camera space 의 좌표를 얻을 수 있다!!

[오른손 좌표계 -> 왼손 좌표계]
z축만 변경해주면 된다.
'ComputerGraphics [고려대학교_한정현]' 카테고리의 다른 글
| Android + OpenGLES로 삼각형 그리기 (0) | 2023.04.02 |
|---|---|
| Android + OpenGLES로 사각형 그리기 (0) | 2023.04.02 |
| 4강(4) 3차원에서 World Transform ( Object Space -> World Space 변환 ) (0) | 2023.03.26 |
| 4강(2) - Transform 3x3행렬의 L구간, T구간 (0) | 2023.03.25 |
| 4강(1)- 변환(transform) - scaling, rotation, translation (0) | 2023.03.25 |



