4강(4) 3차원에서 World Transform ( Object Space -> World Space 변환 )

이번시간에는 3D에서의 Transform 을 배워볼 것이다.

 

 

[3차원 Scaling]

2번쨰 사진 : (2,2,2)배 Scaling    /   3번째 사진, (1/2,1/2,1) 배 Scaling

---

[3차원  Rotation]

 2차원 회전은 항상 '점'중심이었습니다.

 3차원 회전 축을 중심으로 회전합니다.

---

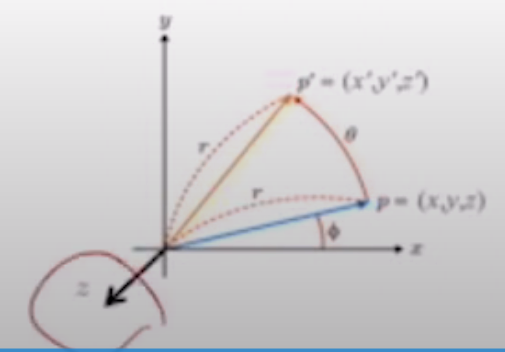
 ex_1) z축 회전

   x랑 y만 변한다. (z좌표는 rotation 후에도 유지된다.)

   R 구간을 변경하면 된다.

 

z축으로 회전한 주전자의 모습

2차원 벡터에서 사용한 회전 설명이다. 여기에 Z축만 생긴것뿐이다.

따라서 값은 2차원 rotation 에서 유도했던 것에 Z축만 동일하게  z로 넣으면 된다.

z축으로 rotation 시키는 행렬

---

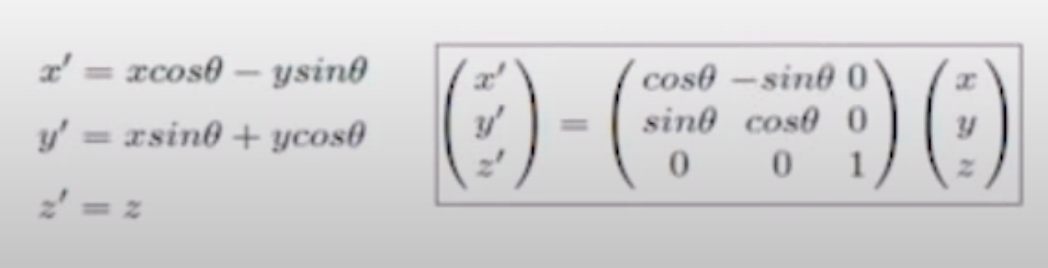
  ex_2) x축 회전

2차원 회전에서 유도한 공식에서 x,y,z,축만 알맞게 변경해서 생각하면 된다.    x축의 역할= y축이됐고, y축의 역할이  z축이 되었을것 이다.

x축 변환의 행렬

---

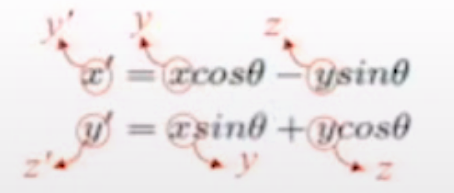
 ex_3) y축 회전

 

---

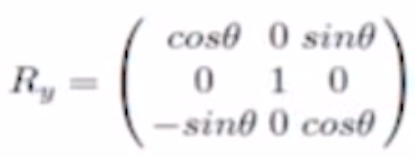
 ex_4) CCW vs CW rotation 

 반시계 방향 회전 Θ가 양수   

 시계방향 회전 은 Θ가 음수로 된다.

---

[3차원 Translation] 

 2차원에서 처럼 사이즈1만큼 더큰 Idnetity행렬을 곱해준다.

 4x4 Identity 행렬에  이동할 만큼의 변위벡터 Dx Dy Dz 만 집어 넣어주면 된다.

---

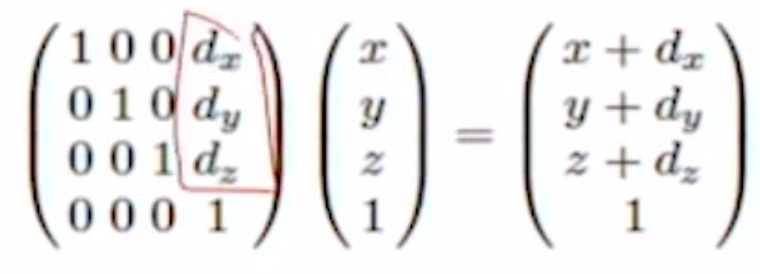
 [ 3차원 변호나을 4X4 곱셈으로 표현하기 ] 

   ex_1) Scaling

노란색 칸처럼 채워주면 된다.

  ex_2) Rotation

  ex_3) Translation 

---

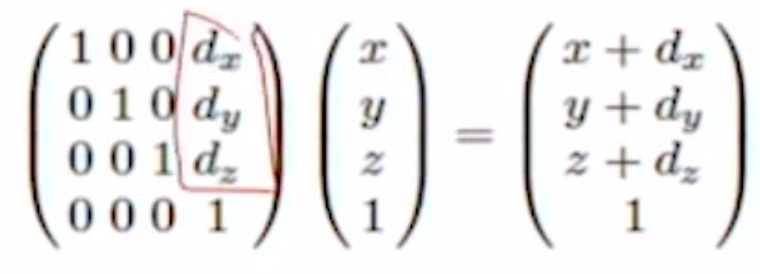
[ World space  /  Object Space ]

 " Object Space" 

 모델링해서 나온 결과물들은 원점을 기준으로 만들어져 있고, 배치되어 져 있다.

  "Word  Space"

 이 결과물들을 실제 게임이나 영화에서의 3차원 공간에 배치해 놓으려면

 적당한 변환을 통해 놓아야한다. 그것이 "월드스페이스" 라고 한다.

 
 "Transform 의 필요성"

 Object Space 에서 World Space 로 옮길때 Transform 이 필요하다.

Transform 을 통해 Wordspace 로 배치시키는 예

 

Transform 을 통해 Wordspace 로 배치시키는 예시 및 Matrix

LT구간 에 대한 설명 :  L 에는 Rotation 에 대한 값만 는것을 확인 할 수 있다. /  L 먼저 적용시키고 , T만큼 이동시키면 됨을 알 수 있다.

---

[Q : T구간은 언제 그대로 나오고 언제 L과 결합되서 나오나요?]

 chat-GPT 답변 :

RT 구간에서 T 구간은 일반적으로 3차원 공간에서 객체의 위치를 변환하는 작업을 의미합니다. T 구간에서는 객체를 이동시키는 변환(translation) 값뿐만 아니라, 회전(rotation) 값과 크기 조절(scale) 값도 포함될 수 있습니다.

따라서, RT 구간에서 T 구간에서 Translation 값만 나오는 경우는 객체를 이동시키는 변환 작업만 수행하고 회전이나 크기 조절 등의 변환 작업을 수행하지 않았을 때입니다. 이 경우, 변환 행렬은 아래와 같이 나타낼 수 있습니다.

|1 0 0 Tx|

|0 1 0 Ty|

|0 0 1 Tz|

|0 0 0 1 |

위 행렬에서 Tx, Ty, Tz는 객체를 이동시키는 변환 값으로, Translation 값과 같은 값을 갖습니다. 그러나 객체의 회전이나 크기 조절 등 다른 변환 작업을 수행했다면 T 구간에서의 변환 값은 Translation 값과 다를 수 있습니다.

---

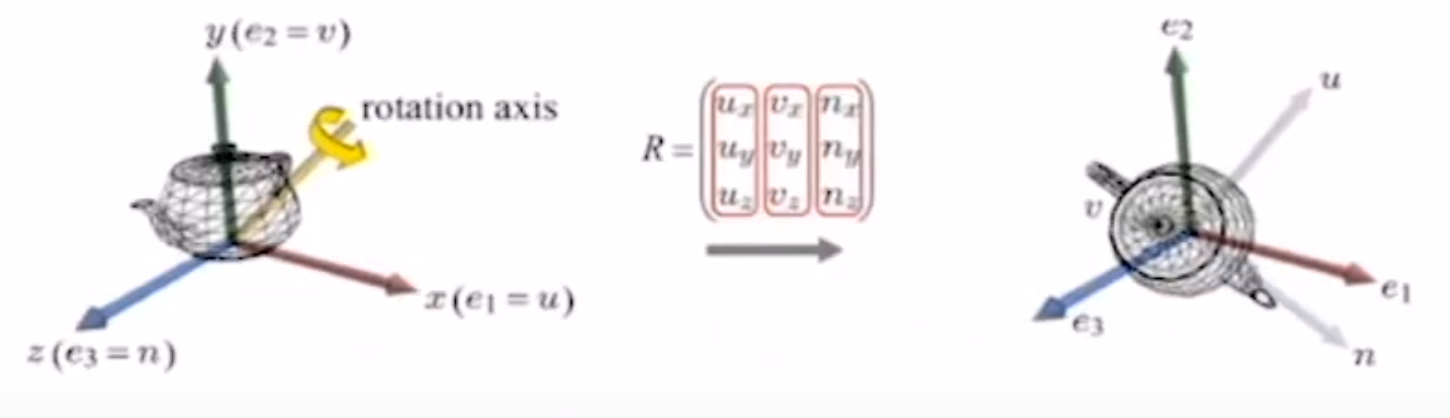
[ Rotation 과  Object Space Basis]

 - Object 와 Object Space 는 항상 딱 붙어있다.

 - 회전은 물체의 방향을 바꾸는 것이다. -> 물체는 object space 와 꽉 붙어있다. -> 회전된 물체의 방향은 object space's basis 의 방향으로 특징 지을 수 있다.

    

 ex_1)  Rotation 예시

   object space : { u, v, n }

   world space :  {e1,e2,e3}

 

   회전 전 : Object Space 와 World Space 는 동일하다.

                              e1 = u  = x축

                              e2 = v  = y축

                              e3 = n  = z축  

   회전 후 : Object Space 와 World Space 는 달라진다.

                              e1 = u n  = x축

                              e2 = v     = y축

                              e3 = n -u  = z축  

회전 후 : world space 축에 매칭되는 object space 의 축들이 바뀌는 것을 알 수 있다.

 - Object Space Basis 인 (u, v, n) 이 알려졌다 > R은 즉각 계산이 가능하다. 

 - R 이 주어졌다.   -> 회전(R)에 의해서 변환된 Object Space Basis 도 바로 알 수 있다. 컬럼 그냥 따오면 된다.

1:15:00 부터 다시듣기

---

[임의의 축에 대한 회전]

 임의의축 에 대한 회전한 object 의 object space basis (u, v, n)을 알 수 있다면, 

 우리는 R(회전) 행렬 을 그냥 구할 수 있다.

u, v, n 을 사용해서 만들어낸 R (회전) Matrix (행렬)